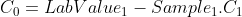The calibration process maps the sensor’s response to an ideal linear response. Depending on the measurements range, offset or linear calibration can be used.
The relationship between a calibrated parameter and its raw equivalent can be then estimated by the equation:

Pcal = Calibrated parameter value
Praw= Sensor measurement of that parameter
C1= Slope
C0 = Offset.
The coefficients C0 and C1 are internally calculated by the Smart Module Electronics Transmitter (SME) during the calibration process. The SME keeps in memory a list of the coefficients that are currently being used, the coefficients that have been calculated by the user in previous calibration operations, and the factory calibration coefficients. Either the factory or user calibration should match with the current calibration coefficients used by the electronics.
Offset Calibration (1-point)
An offset means that the sensor output is higher or lower than the expected reference value. Offset calibration should be used when either the measurements range is kept around a narrow value, or when the sensor response and the ideal response maintain the same behavior within the sensor operation range.
To make an offset calibration one single measurement point can be used. The sensor measurement is then compared with a reference measurement, (a reference instrument for example), and the difference is added to the raw value to obtain the calibrated value.

Linear (Slope and offset) Calibration (2-point )
A slope means that the output changes at a different rate than the ideal rate. Therefore, a two-point calibration should be used to correct the difference between the sensor response and ideal response.

This method should be used when the sensor works in a wide range of measurements and the difference between the ideal response and the sensor response changes linearly within that range.
With the sensor output and the ideal response references, the slope C1 from equation 1 can be calculated as follows:

The C0 coefficient can be estimated evaluating the equation 1, in the 1st point taken.